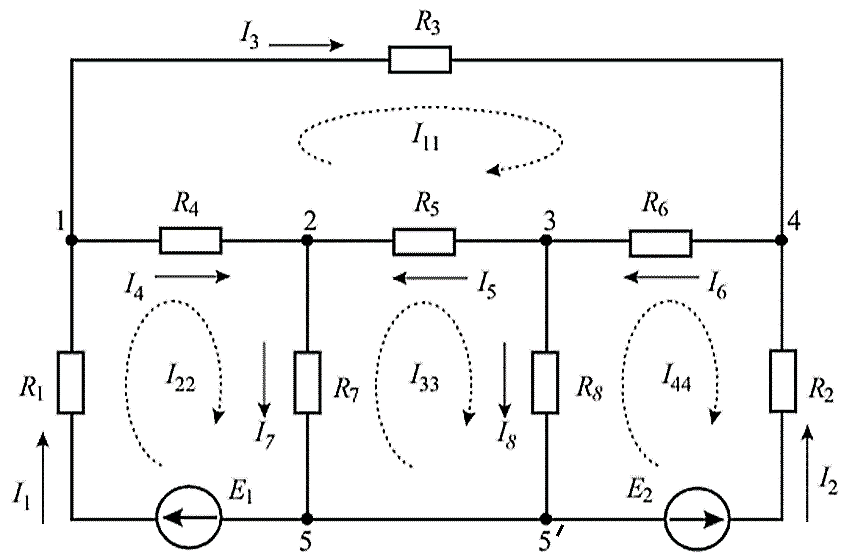
Пусть имеется электрическая цепь постоянного тока, представленная на рис. 1. Напишем программу в Python для определения токов в ветвях этой цепи. Задачу будем решать методом контурных токов.
Исходные данные:
Е1=145 В, Е2=140 В, R1=R2=1 Ом, R3=0.5 Ом, R4=10 Ом, R5=4 Ом, R6=1 Ом, R7=8 Ом, R8=5 Ом.
Приведем вначале несколько определений.
Ветвью называется участок электрической цепи между двумя узлами. Во всех элементах (резисторах) ветви протекает одинаковый ток.
Узлом называется место соединения трех и более ветвей.
Контуром называется замкнутый участок электрической цепи, состоящий из нескольких ветвей.
Контурный ток – это величина, которая одинакова во всех ветвях выбранного контура. Контурный ток обычно обозначают двойными индексами, например I11, I22 и т.д. Направление контурного тока выбирается произвольно, например, по часовой стрелке.
Для составления уравнений по методу контурных токов используется второй закон Кирхгофа, который гласит: алгебраическая сумма ЭДС в любом замкнутом контуре равна алгебраической сумме падений напряжений на элементах этого контура:
Σ Ii · Ri = Σ Ei
где i – номер элемента (резистора или источника напряжения) в контуре.
Число уравнений, составляемых по методу контурных токов, определяется по формуле:
N = Nв – (Nу – 1) – Nи.т.
где Nв – число ветвей электрической цепи;
Nу – число узлов;
Nи.т. – число источников тока ( в представленной на рис. 1 электрической цепи источников тока нет).
ЭДС, направление которых совпадает с направлением контурного тока, записывают со знаком «+», если не совпадает, то со знаком “–”.
Действительный ток в ветви определяется алгебраической суммой контурных токов, в которую эта ветвь входит.
Последовательность решения задачи следующая:
1 – Определение числа уравнений и, следовательно, количества независимых контуров.
2 – Задание направлений действительных и контурных токов.
3 – Составление уравнений для нахождения контурных токов.
4 – Решение уравнений и нахождение контурных токов.
5 – Нахождение действительных токов.
Приступим к решению задачи. Определим число уравнений. Следует иметь в виду, что точки 5 и 5′ принадлежат одному разнесенному в пространстве узлу.
N = 8 – (5 – 1) = 4
Получаем четыре независимых контура. Проставляем направления действительных и контурных токов, как показано на рис. 1. Переходим к составлению уравнений.

В полученном решении должен выполняться баланс мощностей, а именно: сумма мощностей, выделяемых источниками, равна сумме мощностей, потребляемых приемниками Σ Рист = Σ Рпр, где
Σ Рист – сумма мощностей источников напряжения;
Σ Рпр – сумма мощностей, потребляемых приемниками.
Для электрической цепи на рис. 1 равенство мощностей запишется следующим образом:

Если направление ЭДС и тока через ЭДС совпадают, то произведение (E·I) берется со знаком “+”, если не совпадает, то со знаком “–”. В нашем случае направления ЭДС и тока совпадают.
Запрограммируем в Python полученные уравнения. Матричное уравнение (4) решаем с помощью стандартной библиотеки numpy. Листинг программы имеет следующий вид:

Программа выдает следующие результаты:
IK= [ 10. 15. 5. -15.]
I1= 15.0 I2= 15.0 I3= 10.0
I4= 5.0 I5= 5.0 I6= 25.0
I7= 10.0 I8= 20.0
Pit= 4275.0 Ppr= 4275.0
Баланс мощностей выполняется: 4275 вт = 4275 вт, следовательно, задача решена верно.
Вывод. Требуется всего три строчки кода, чтобы с помощью стандартной библиотеки numpy решить матричное уравнение и найти контурные токи.