Напишем программу в Python для расчета токов в ветвях электрической цепи постоянного тока, содержащей источники напряжения и источник тока. В предыдущей статье “Py13. Расчет электрической цепи в Python методом контурных токов. Пример 1” была рассмотрена электрическая цепь, содержащая только источники напряжения. Добавим в эту цепь источник тока, как показано на рис. 1. Определим токи в ветвях этой цепи. Задачу будем решать, как и в предыдущем случае, методом контурных токов.
Исходные данные:
Е1=145 В, Е2=140 В, R1=R2=1 Ом, R3=0.5 Ом, R4=10 Ом, R5=4 Ом, R6=1 Ом, R7=8 Ом, R8=5 Ом, J= 10 А.
К использовавшимся ранее исходным данным добавился ток J = 10 А от источника тока.

По формуле (1) определяем число уравнений, необходимых для решения задачи.
N = Nв – (Nу – 1) – Nи.т. (1)
где Nв – число ветвей электрической цепи;
Nу – число узлов;
Nи.т. – число источников тока.
N = 9 – (6 – 1) – 1 = 3
Итак, для решения задачи требуется три уравнения и, следовательно, надо выбрать три независимых контура. Контуры надо выбирать таким образом, чтобы в них не входил источник тока. Выберем контуры: 1, 2, 3, и укажем в них направления контурных токов: I11, I22, I33. Средний контур (между контурами 2 и 3) в составлении уравнений участвовать не будет, но направление тока J в этом контуре нам понадобится, поэтому задаем в этом контуре направление тока J. Далее указываем направления действительных токов, как показано на рис. 1, и переходим к составлению уравнений.
Напомним правила, которые надо соблюдать при составлении уравнений по методу контурных токов. Стрелка внутри графического символа источника напряжения показывает направление действия ЭДС и направлена от точки с низшим потенциалом к точке с высшим потенциалом. Если направление действия ЭДС совпадает с направлением контурного тока, то берем знак (+), если не совпадает, то берем (–). На зажимах источника возникает напряжение (U), которое принято направлять от положительного потенциала к отрицательному, т.е. в сторону обратную действию ЭДС. При этом выполняется равенство U = E. При составлении баланса мощностей, если ток в источнике протекает в том же направлении, что и действие ЭДС, то источник отдает энергию во внешнюю цепь, если в противоположном, то источник получает энергию из цепи от других источников. Мощность, которую отдает (или получает) источник напряжения определяется произведением: P = ± E·I, где Е – ЭДС, I – ток.
Угловые скобки внутри графического символа источника тока указывают на направление тока. Если направление тока источника совпадает с направлением контурного тока в цепи, то берем знак (+), если не совпадает, то берем знак “–”. Если в результате решения задачи оказывается, что ток и напряжение на источнике тока направлены в разные стороны, то источник отдает энергию в цепь, если направлены в одну сторону, то источник получает энергию из цепи от других источников. Мощность, которую отдает (или получает) источник тока определяется произведением: P = ± J·Uj , где Uj – напряжение на источнике тока.

При балансе мощностей должно выполняться равенство: Σ Рист = Σ Рпр, где
Σ Рист – сумма мощностей источников напряжения и источников тока;
Σ Рпр – сумма мощностей, потребляемых приемниками.
Чтобы записать баланс мощностей для электрической цепи на рис. 1, необходимо найти напряжение на источнике тока. Для определения напряжения на источнике запишем равенство:
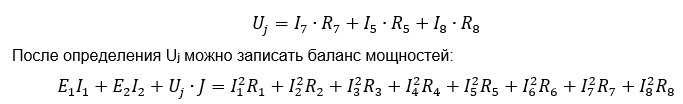
Запрограммируем в Python полученные уравнения. Матричное уравнение (5) решаем с помощью стандартной библиотеки numpy. Листинг программы имеет вид:

Программа выдает на печать следующие результаты:
IK= [ 14.42085661; 19.4320298; -10.79702048]
I1= 19.43; I2= 10.8; I3= 14.42;
I4= 5.01; I5= –4.42; I6= 25.22;
I7= –9.43; I8= 20.8
Pit= 4437.68156424581; Ppr= 4437.6815642458105
Кроме баланса мощностей должен выполняться первый закон Кирхгофа для всех узловых точек. В нашем случае баланс мощностей и первый закон Кирхгофа выполняются, следовательно, задача решена верно.