В предыдущих статьях Py14 и Py13 метод контурных токов применялся для расчета электрических цепей постоянного тока. В этой статье применим метод контурных токов для расчета электрической цепи переменного тока. Электрическая цепь переменного тока представлена на рис. 1. Эта цепь аналогична рассмотренной ранее в статье “Py12. Расчет цепей переменного тока в Python. Пример 2”. Однако ранее задача решалась методом эквивалентных сопротивлений, сейчас будем решать ту же задачу методом контурных токов. Использование одной и той же электрической схемы позволит сравнить результаты двух подходов к решению задачи и избежать возможных ошибок. Вместе с тем, метод контурных токов является более универсальным, чем метод эквивалентных сопротивлений, и позволяет рассчитывать более сложные электрические цепи, поэтому так важно уметь пользоваться этим методом.
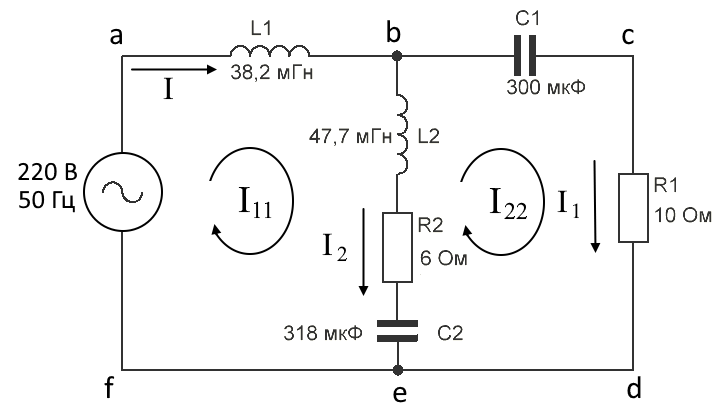
Цепь имеет следующие параметры:
E = 220 В; f = 50 Гц; L1 = 38,2 мГн; L2 = 47,7 мГн; R1 = 10 Ом; R2 = 6 Ом; С1 = 300 мкФ; С2 = 318 мкФ.
Найти токи: I; I1; I2.
Решение задачи начинаем с определения числа уравнений, необходимых для решения задачи.
N = Nв – (Nу – 1) – Nи.т. = 3 – (2–1) – 0 = 2
где Nв – число ветвей электрической цепи;
Nу – число узлов;
Nи.т. – число источников тока.
Итак, для решения задачи надо записать два уравнения. Запишем систему из двух уравнений. При записи уравнений используем символический метод (точка сверху над электрическими параметрами означает комплексную величину):

Для решения матричного уравнения (2) используем стандартную библиотеку numpy.
После того, как будут найдены контурные токи, переходим к вычислению токов в электрических ветвях:
I=abs(I11 );
I1=abs(I22 );
I2=abs(I11-I22 );
Листинг программы имеет вид:

Программа выводит на печать следующие результаты:
IK= [6.4455692 -13.23420224j 6.73873682 -0.58523095j]
I= 14.72;
I1= 6.764;
I2= 12.652.
Таким образом, результаты, полученные в этой статье, совпадают с результатами, полученными в статье Py12, что говорит о корректности приведенного решения.