Суть наведения ракеты на цель по методу пропорционального сближения заключается в том, что угловая скорость вращения вектора линейной скорости ракеты относительно оси z, направленной перпендикулярно плоскости чертежа, пропорциональна угловой скорости вращения линии визирования цели:
ωp = k ωc (1)
где
ωp, ωc – угловые скорости вращения вектора скорости ракеты и линии визирования соответственно;
k – коэффициент пропорциональности.
Этот метод наведения является в настоящее время основным для самонаводящихся ракет.
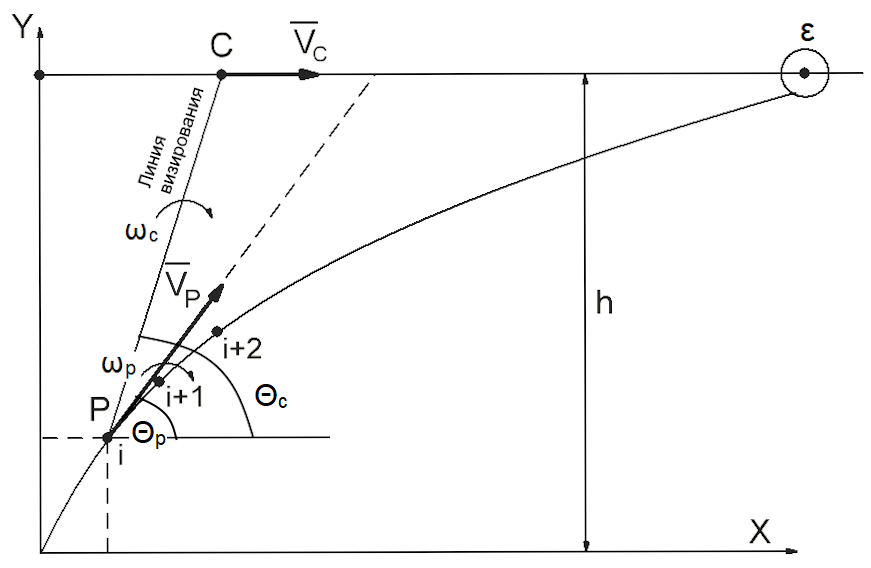
Задачу будем рассматривать в рамках плоской системы координат x, y (рис. 1).
Цель (точка С) движется с постоянной скоростью Vc прямолинейно на высоте h. Ракета (точка Р) движется с постоянной скоростью Vp. Запишем систему уравнений движения для цели и ракеты и решим её численно.
Система уравнений имеет следующий вид:

Запрограммируем уравнения системы (3) и построим график траектории ракеты.
Листинг программы на Python имеет вид:

Результаты расчетов.
Воспроизведем вначале траекторию, которая была получена по методу погони в предыдущей статье: “Кинематический расчет траектории при наведении на цель по методу погони”. Траектория по методу погони получается, как частный случай из приведенной здесь программы, если положить k=1.

Из рис. 2 видно, что при методе погони ракета заходит в хвост цели и догоняет её сзади.
А теперь зададим k=8, а остальные исходные данные оставим без изменений. Результаты расчета для этого случая представлены на рис. 3.
Из рис. 3 видно, что после начального участка траектории, в дальнейшем, ракета движется к цели по прямой и подходит к ней с нижней полусферы. Кроме того, сокращается подлетное время ракеты к цели. Таким образом, траектория по методу пропорционального сближения кардинальным образом отличается от траектории по методу погони. Очевидно также, что в этом случае улучшаются вероятностные характеристики поражения цели.
Давайте зададим в программе исходные данные, примерно соответствующие реальным скоростям полета цели и ракеты:
vc = 320 м/с – скорость цели (самолета);
vp = 560 м/с – скорость ракеты от ПЗРК.
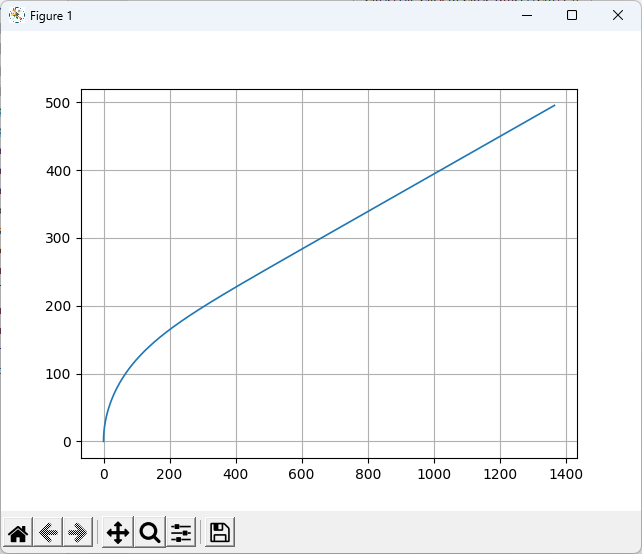
График траектории для этих исходных данных приведен на рис. 4.

Углы наклона линии визирования (обозначен в программе, как tetac) и наклона вектора скорости ракеты (обозначен в программе, как tetap) для траектории полета, представленной на рис. 4, показаны на рис. 5. На графике (рис. 5) по оси ординат отложен угол в радианах, по оси абсцисс – координата Х ракеты. Из рис. 5 видно, что углы на большей части траектории сохраняют постоянные значения.
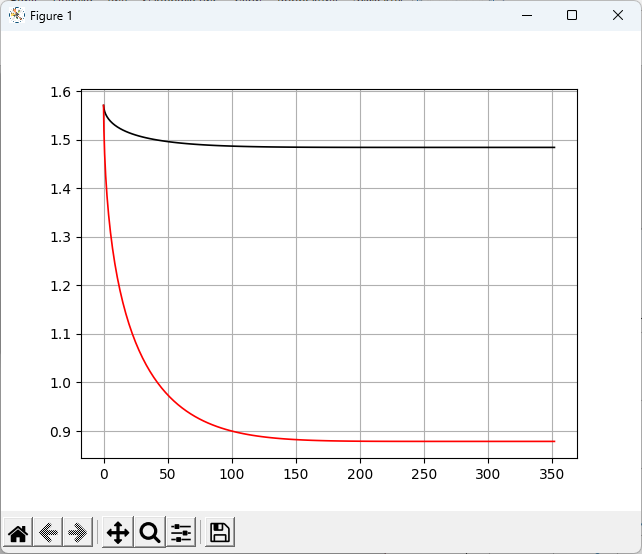
Параметры в конце траектории ракеты в момент окончания расчета имеют следующие значения:
t= 1.1 сек – время подлета ракеты;
xp= 352 м – координата Х ракеты;
yp= 497 м – координата Y ракеты;
tetac= 85º – угол наклона линии визирования;
tetap= 50º – угол наклона вектора скорости ракеты.
Предложенное решение позволяет, в первом приближении, проанализировать координатно-временные характеристики траектории самонаводящейся ракеты.