Прежде, чем переходить к предлагаемому в данной статье примеру (Схема 2), ознакомьтесь вначале с примером: “Py11. Расчет цепей переменного тока в Python (Схема 1).
Рассчитаем символическим методом цепь переменного тока, представленную на рис. 1.
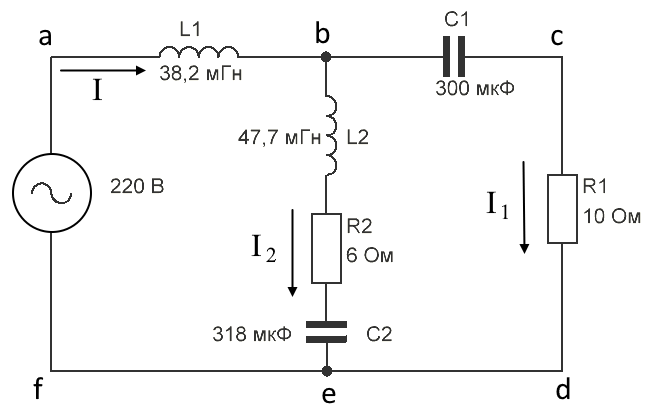
Цепь имеет следующие параметры:
U = 220 В, f = 50 Гц, L1 = 38,2 мГн, R2 = 6 Ом, С2 = 318 мкФ, L2 = 47,7 мГн, R1 = 10 Ом, С1 = 300 мкФ.
Найти:
– токи: I; I1; I2;
– выходное напряжение Uout (напряжение на резисторе R1)
В таблице 1 приведены формулы для расчета комплексных сопротивлений:

В таблице 2 приведены формулы для расчета параметров электрической цепи, показанной на рис. 1. Комплексные напряжения и ток помечены точкой сверху, комплексные сопротивления помечены подчеркиванием.

Формулы в таблице 2 записаны с использованием закона Ома и с использованием правил вычисления сопротивлений при последовательном и параллельном соединении.
Запрограммируем в Python зависимости (1) … (12).
Листинг программы имеет вид:

Программа выводит на печать результаты:
IT = 6.45 – 13.23j
IT1= 6.74 – 0.59j
IT2 = –0.29 – 12.65j
UTout = 67.39–5.85j
I= 14.72
I1= 6.764
I2= 12.652
Uout= 67.641
Проверяем первый закон Кирхгофа для комплексных токов: сумма действительных частей комплексов входящих токов должна быть равна сумме действительных частей комплексов выходящих токов и, соответственно, сумма мнимых частей комплексов входящих токов должна быть равна сумме мнимых частей комплексов выходящих токов,
6.45 – (6.74 – 0.29) = 0 для действительных частей;
–13.23 – (–0.59 – 12.65) = 0.01 для мнимых частей.
С точностью до ошибок округления первый закон Кирхгофа для комплексных токов выполняется.
Итак, в результате решения получены следующие значения токов и напряжений:
I = 14.72 А – полное действующее значение тока;
I1 = 6.764 А – действующее значение тока в ветви bcd электрической цепи;
I2 = 12.652 А – действующее значение тока в ветви be электрической цепи;
Uout = 67.641 В – выходное напряжение цепи.